PARADIGME DIN POST-IZOLARE – Robert MARIN – Conturul material

1. Conturul și spațiul

Atunci cînd vorbim de geometrie ne referim cel mai des la forma unui solid, la suprafețe clar determinate  ce separă un obiect de mediu. Într-o astfel de situație ideea de contur reprezintă proiecția perimetrului acestei forme, vizibil dintr-un anumit punct de observare. Dar nu toate obiectele au aparența organizată a unui cristal, unele forme sunt încurcate, instabile, au alcătuiri extrem de complexe. Uneori obiectele sunt atît de ambigue încît rămîn neîncadrabile într-un contur, fie el chiar unul dinamic. Alteori conturul este singura caracteristică observabilă a unei forme. Artele vizuale s-au luptat cu natura inconsecventă a conturului de la segmentările Cubismului și reprezentarea mișcării în Futurismul din prima parte a secolului XX pînă la mai recente încercări artistice paramentrice de tip „wireframe” sau „point cloud”. Unul dintre artiștii contemporani celebri care au explorat în mod poetic relația dintre contur și spațiul tridimensional este britanicul Antony Gormley. În imaginile de mai jos două lucrări pe această temă: „Clearing VII” și „Feeling Material XIV”.

 

Prima lucrare este o singură linie din kilometri de bară rectangulară subțire, fără început și fără sfîrșit. Este un desen în spațiu ce se răsucește tensionat între pereții, plafonul și pardoseala galeriei. Această mîzgăleală metalică 3D ocupă spațiul determinînd o serie de parcursuri posibile ale observatorului, un contur al interacțiunii.   În a doua lucrare artistul realizează o siluetă ambiguă în spațiu prin excedent de linie, prin înglobarea în forma descrisă a numeroase trasee, modulări, posibile contururi. Astfel de utilizări a liniei ca perimetru al unor forme imateriale propune o descompunere a conceptelor monolit cu care aproape toți descriem realitatea fizică ce ne înconjoară.  Într-un fel întreaga operă a sculptorului britanic este o deconstrucție sau o reinterpretare a noțiunii de „corp”prin favorizarea ideii de spațiu și diminuarea celei de limită. Iată un scurt exercițiu prin care Gormley prezintă unui auditoriu interesat efortul artistic pe care îl întreprinde, de menționat că problematica sculpturii pe care o atacă este mult mai amplă decît noțiunea de contur. „Închideți ochii pentru un minut. Iată-ne într-un spațiu subiectiv, colectiv, un spațiu al întunericului corpului. Mă gîndesc la acest loc ca la un cîmp al imaginației, al potențialului, dar care sunt calitățile lui? Este fără obiect – nu este nimic în el, este fără dimensiune – nu are limite. Deschideți ochii. Acesta este spațiul în care gîndesc sculptura – ceea ce este puțin paradoxal pentru că sculptura este despre a face propuneri materiale – dar cred că acesta este spațiul pe care sculptura îl poate conecta cu noi”. Dacă aveți timpul necesar puteți vedea întreaga prezentare aici: https://www.ted.com/talks/antony_gormley_sculpted_space_within_and_without#t-304692

 

2. Un contur contraintuitiv

„Dacă adevărurile logice sunt adevărate independent de stările și aranjamentele din lume atunci, iată un gînd neliniștitor, poate că ele nu sunt descrieri ale lumii ci limitele ei, poate că acesta este conturul a ceea ce în mod inteligibil poate fi situat în lume.” Acest citat a fost extras (și adaptat) din emisiunea „In Our Time” de pe BBC Radio 4 în care Melvyn Bragg i-a avut invitați pe profesorii și conferențiarii de filosofie Ray Monk, Barry Smith și Marie McGinn pentru a discuta despre opera lui Ludwig Wittgenstein, pentru cei interesați iată întreaga conversație aici: https://www.youtube.com/watch?v=XB3OwIV5oro Adevărurile matematice au fost invidiate de-a lungul istoriei, probabil în special de filosofi, pentru gradul de certitudine pe care l-au revendicat atît de des. În unele cazuri corespondența cu realitatea este evidentă (un măr + un măr = două mere), în alte cazuri este necesar un salt imaginar spectaculos deseori acceptat doar la nivel de convenție (numerele imaginare), dar sunt situații curioase în care intuiția ne aruncă atît de departe de soluția matematică a problemei încît și cea mai exactă dintre științe pare neconvingătoare. În acest ultim caz este înțelept să luăm distanță față de intuițiile noastre și să încercăm să alcătuim un răspuns rațional verificabil.

Am găsit undeva pe net o problemă de testare a intuiției referitoare la conturul lucrurilor pe care se spune că Ludwig Wittgenstein o încerca pe studenții lui, ea sună cam așa. Să ne închipuim că Pămîntul este perfect sferic și că îl înconjurăm pe la ecuator cu un fir de metal lipit de suprafața sa, obținem practic un cerc cu aceeași rază cu cea a Pămîntului. Acum adăugăm un metru la lungimea acestui fir metalic și îi refacem forma de cerc care se va depărta echidistant de suprafața Pămîntului. Întrebarea este: cu cît credeți că s-a depărtat firul (depărtare constantă la scară planetară) de suprafața sferei? Este această distanță neglijabilă, aproape egală cu zero? Sau putem spune, de exemplu, că ne încape mîna pe sub firul paralel cu planeta? Toți cei cărora le-am ridicat această problemă (eu evident instalat într-o poziție superioară total nemeritată) au comparat intuitiv dimensiunile colosale ale unei sfere de mărimea Pămîntului cu bietul metru adăugat la circumferința acestui imens cerc și au concluzionat că firul rămîne practic lipit de planetă. Cum ar putea, în mod substanțial, un surplus atît de mic să afecteze un contur atît de mare. Răspunsul matematic este că firul lungit cu un metru se depărtează pe toată circunferința sferei planetare cu 15,92 cm, cam cît să încapă o mînă.

Iată și formalizarea problemei și rezolvarea matematică. Notăm cu C1 circumferința Pămîntului și cu R1 raza corespunzătoare, notăm cu C2 noua circumferință care este egală cu C1 + 100 cm căreia îi corespunde raza R2. A se afla distanța d, distanță constant egală cu R2 – R1 în situația în care cele două cercuri sunt concentrice.

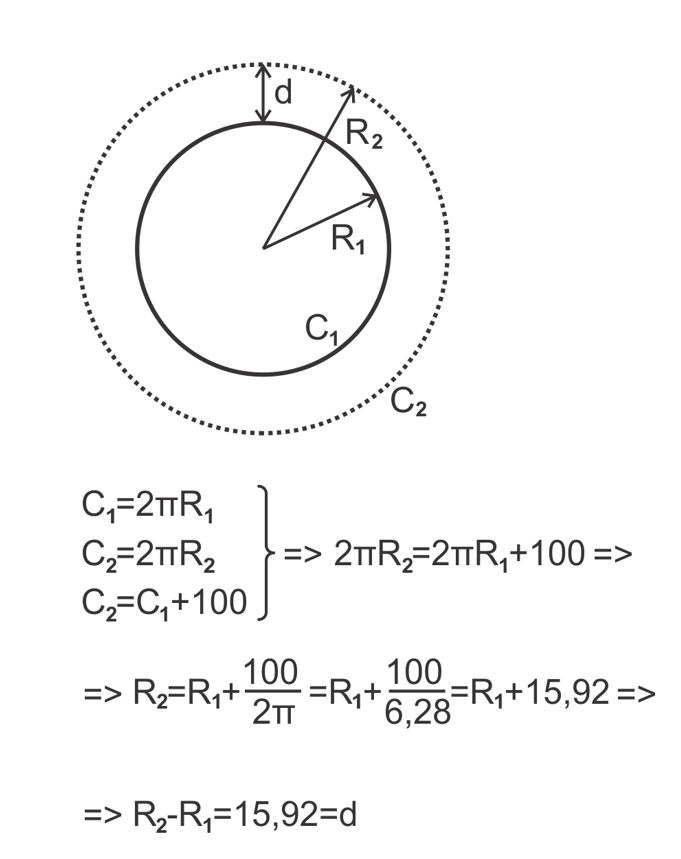
O observație interesantă este că distanța dintre cercuri este o funcție a modificării circumferinței independentă de valoarea nominală a razei cercului inițial. Ceea ce înseamnă că dacă adăugăm 100 de centimetri la conturul unei mingi de ping-pong noul cerc se va depărta de cel inițial tot cu 15,92 cm. A nu se înțelege de aici că orice gest pe care îl facem ar trebui determinat matematic, pînă la urmă se pare că Wittgenstein era destul de nemulțumit de încrederea oarbă pe care oamenii începuseră să o investească în știință la începutul secolului XX. Ce ne sugerează o astfel de situație este necesitatea unui spirit dilematic mai activ și o curiozitate susținută cu un instrumentar de cercetare cît mai larg.

ROBERT  MARIN este absolvent de Arhitectură și de… „Carabellă” târgovișteană.